Lineare Kontrolltheorie – Regelbarkeit und Stabilisierbarkeit

Regelbarkeit und die Kalman-Matrix

Gegeben seien ein LTI-System \(\dot {x} = Ax + Bu\), \(x(0) = \xi \in \real ^n\) mit \(A \in \real ^{n \times n}\) und \(B \in \real ^{n \times m}\) sowie ein fester Zeitpunkt \(T > 0\). Im Folgenden soll untersucht werden, welche Zustände zur Zeit \(T\) erreicht werden können, indem man eine geeignete Steuergröße \(u(\cdot )\) verwendet.

Weil \(x(T) = e^{AT} \xi + \int _0^T e^{A(T - \tau )} Bu(\tau ) \d \tau \) gilt und der erste Summand nicht von \(u(\cdot )\) abhängt, reicht es aus, die möglichen Werte von \(\int _0^T e^{A(T - \tau )} Bu(\tau )\d \tau \) zu analysieren (also für \(\xi = 0\)).

erreichbare Menge: Die erreichbare Menge (reachable set) \(\R _T\) von \(\dot {x} = Ax + Bu\) zur Zeit \(T > 0\) ist die Menge aller Zustände \(x(T)\), die vom Null-Anfangswert durch einen stetigen Steuereingang erreicht werden können, also \(\R _T := \left \{\left .\int _0^T e^{A(T - \tau )} Bu(\tau )\d \tau \;\right | u \in \C ([0, T], \real ^m)\right \}\).

Zunächst benötigt man ein paar Definitionen aus der linearen Algebra. Sei dazu \(A \in \real ^{n \times p}\).

Bildraum: Der Bildraum (range space) \(R(A) := \{Ax \;|\; x \in \real ^p\}\) ist die Menge aller Linearkombinationen der Spalten von \(A\).

Nullraum: Der Nullraum (null space) oder Kern ist \(N(A) := \{x \in \real ^p \;|\; Ax = 0\}\).

Zeilen-/Spaltenrang: Es gilt \(R(A) = \real ^n\) genau dann, wenn \(A\) vollen Zeilenrang hat.
Es gilt \(N(A) = \{0\}\) genau dann, wenn \(A\) vollen Spaltenrang hat.

orthogonales Komplement des Bilds: Es gilt \(N(A^T) = R(A)^\bot \).

Cayley-Hamilton: Für \(A \in \real ^{n \times n}\) quadratisch und \(k \in \natural _0\) ist die \(k\)-te Potenz \(A^k\) eine Linearkombination von \(I, A, \dotsc , A^{n-1}\), da \(\chi _A(A) = 0\) mit \(\chi _A\) dem charakteristischen Polynom von \(A\).

Beobachtung: Für \(u \in \C ([0, T], \real ^m)\) gilt, dass \(x(T) = \int _0^T e^{A(T-\tau )} B u(\tau ) \d \tau = \lim _{N \to \infty } x_N\) mit \(x_N := \int _0^T \sum _{k=0}^N \frac {1}{k!} [A(T - \tau )]^k Bu(\tau )\d \tau \), weil die Potenzreihe des Matrixexponentials gleichmäßig konvergiert. \(x_N\) lässt sich umschreiben zu \(x_N = \sum _{k=0}^N A^k B \cdot \left [\int _0^T \frac {(T - \tau )^k}{k!} u(\tau )\d \tau \right ]\). Der Ausdruck in eckigen Klammern ist ein Vektor \(v_k \in \real ^m\), d. h. \(x_N\) ist eine Linearkombination der Spalten von \(B, AB, \dotsc , A^N B\). Weil alle Matrizen \(A^n, A^{n+1} B, \dotsc , A^N B\) wegen Cayley-Hamilton Linearkombinationen von den Matrizen \(B, AB, \dotsc , A^{n-1} B\) sind, ist \(x_N\) für alle \(N \in \natural _0\) eine Linearkombination der Spalten von \(B, AB, \dotsc , A^{n-1} B\) d. h. \(x_N \in R\smallpmatrix {B & AB & \cdots & A^{n-1} B}\). Im Grenzübergang gilt daher auch \(x(T) \in R\smallpmatrix {B & AB & \cdots & A^{n-1} B}\), weil \(R\smallpmatrix {B & AB & \cdots & A^{n-1} B}\) als endlich-dimensionaler Unterraum topologisch abgeschlossen ist.

Kalman-Matrix: Die Kalman-Matrix oder Regelbarkeitsmatrix (controllability matrix) für das lineare System \(\dot {x} = Ax + Bu\) (oder das Paar \((A, B)\)) ist definiert durch \(K := \smallpmatrix {B & AB & \cdots & A^{n-1} B}\).

Gerade wurde gezeigt, dass \(\R _T \subset R(K)\). Allerdings gilt sogar Gleichheit.

Regelbarkeits-Gram-Matrix: Die Regelbarkeits-Gram-Matrix (controllability Gramian) von
\((A, B)\) zur Zeit \(T > 0\) ist \(W_T := \int _0^T e^{At} BB^T e^{A^Tt}\dt = \int _0^T e^{A(T-\tau )} BB^T e^{A^T(T-\tau )}\d \tau \in \real ^{n \times n}\).

Weil die Einträge von \(e^{At} BB^T e^{A^Tt}\) Linearkombinationen von Termen der Form \(t^k e^{\lambda t}\) sind, kann man \(W_T\) explizit ausrechnen.

Lemma: \(W_T\) ist symmetrisch und positiv semidefinit. Außerdem gilt \(R(W_T) = R(K)\).

Konstruktion von Steuergrößen: Sei \(x_f \in R(K)\) beliebig. Dann gibt es nach dem Lemma ein \(\alpha \in \real ^n\) mit \(x_f = W_T \alpha \). Mit der Steuergröße \(u(\tau ) := B^T e^{A^T (T - \tau )} \alpha \) erhält man
\(x(T) = \int _0^T e^{A(T - \tau )} Bu(\tau ) \d \tau = \int _0^T e^{A(T - \tau )} B B^T e^{A^T (T - \tau )} \alpha \d \tau = W_T \alpha = x_f\). Also steuert diese Steuergröße vom Nullzustand in den Zustand \(x_f\) zur Zeitpunkt \(T\), d. h. \(x_f \in \R _T\). Daher gilt auch die Umkehrung der obigen Inklusion: \(R(K) \subset \R _T\).

Satz (erreichbare Menge ist das Bild der Kalman-Matrix):
Es gilt \(\R _T = R(K)\) mit der Kalman-Matrix \(K := \smallpmatrix {B & AB & \cdots & A^{n-1} B}\).

Daher ist \(\R _T\) ein Unterraum von \(\real ^n\), der sogar unabhängig von \(T > 0\) ist. Man schreibt deswegen \(\R := R(K)\).

regelbar: Das lineare System \(\dot {x} = Ax + Bu\) (oder das Paar \((A, B)\)) heißt regelbar (controllable), falls \(\R = \real ^n\).

Satz (Kalman-Test zur Regelbarkeit): Das System definiert durch \((A, B)\) ist regelbar genau dann, wenn die Kalman-Matrix \(K := \smallpmatrix {B & AB & \cdots & A^{n-1} B}\) vollen Zeilenrang hat.

Punkt-zu-Punkt-Regelung

Wenn man versucht, \(x_f \in \real ^n\) von einem Anfangswert \(\xi \in \real ^n\) mit \(\xi \not = 0\) zu erreichen, dann muss eine Steuergröße \(u(\cdot )\) gefunden werden, sodass gilt: \(x_f = e^{AT}\xi + \int _0^T e^{A(T-\tau )} Bu(\tau ) \d \tau \), d. h. \(x_f - e^{AT}\xi \in \R \).

Satz (Punkt-zu-Punkt-Regelung): Der Zustand \(x(0) = \xi \) kann in den Zustand \(x(T) = x_f\) (\(T > 0\)) geregelt werden genau dann, wenn \(x_f - e^{AT} \xi \in R(K)\).

Durch die Beweise kann man die notwendige Steuergröße \(u(\cdot )\) sogar explizit angeben.

Folgerung: Bei regelbaren Systemen kann man von jedem Anfangszustand \(\xi \in \real ^n\) zur Zeit \(0\) zu jedem Endzustand \(x_f \in \real ^n\) zur Zeit \(T > 0\) steuern.

Bemerkung: Falls \(A\) invertierbar ist und \((x_1, u_1)\), \((x_2, u_2)\) Gleichgewichte von \(\dot {x} = Ax + Bu\) sind, dann kann man von \(x_1\) zu \(x_2\) steuern,
denn \(x_2 \in R(K)\) (nach Cayley-Hamilton gilt \(A^{-1} = -\frac {1}{\alpha _n} (A^{n-1} + \alpha _1 A^{n-2} + \dotsb + \alpha _{n-1} I)\) mit \(\chi _A(\lambda ) = \lambda ^n + \alpha _1 \lambda ^{n-1} + \dotsb + \alpha _n\), daraus folgt \(x_2 = -A^{-1} Bu_2 \in R(K)\))
und \(e^{AT} x_1 \in R(K)\) (da \(e^{AT} x_1 = \sum _{k=0}^\infty \frac {T^k}{k!} (A^k x_1)\) mit \(A^k x_1 \in R(K)\), weil \(x_1 \in R(K)\) und \(R(K)\) \(A\)-invariant ist, daraus folgt \(e^{AT} x_1 \in R(K)\), weil \(R(K) \subset \real ^n\) abgeschlossen ist).
Somit ist \(x_2 - e^{AT} x_1 \in R(K)\).

Eigenschaften der Kalman-Matrix

Satz (geometrische Charakterisierung von \(\R \)):
\(\R = R(K)\) ist der kleinste \(A\)-invariante Teilraum, der \(R(B)\) enthält.

Die Zustandskoordinaten-Transformation \(z = Tx\) des Systems \(\dot {x} = Ax + Bu\), \(y = Cx + Du\) mit \(T\) invertierbar führt zu \(\dot {z} = \widetilde {A} z + \widetilde {B} u\), \(y = \widetilde {C} z + \widetilde {D} u\) mit \(\smallpmatrix {\widetilde {A} & \widetilde {B} \\ \widetilde {C} & \widetilde {D}} := \smallpmatrix {TAT^{-1} & TB \\ CT^{-1} & D}\). Man sieht schnell, dass die Kalman-Matrix \(\widetilde {K}\) des transformierten Systems bestimmt ist durch \(\widetilde {K} := TK\), wobei \(K\) die Kalman-Matrix von \((A, B)\) ist.

Lemma (Koordinatentransformation): Die Kalman-Matrizen \(K\) von \((A, B)\) und \(\widetilde {K}\) von \((\widetilde {A}, \widetilde {B})\) hängen zusammen durch \(\widetilde {K} = TK\). Daher ist Regelbarkeit invariant unter Zustandskoordinaten-Transformation.

Regelbar-kanonische Form (SI-Systeme)

SI-System: Ein SI-System (single-input system) ist ein System \(\dot {x} = Ax + Bu\) mit \(m = 1\).

regelbar-kanonische Form: Ein SI-System \(\dot {x} = \widetilde {A}x + \widetilde {B}u\) mit
einer Begleitmatrix \(\widetilde {A} := \smallpmatrix {-\alpha _1 & -\alpha _2 & \cdots & -\alpha _n \\ 1 & 0 & & & \\ & \ddots & \ddots & & \\ 0 & & 1 & 0}\) und dem ersten Einheitsvektor \(\widetilde {B} := \smallpmatrix {1 \\ 0 \\ \vdots \\ 0}\)
heißt in regelbar-kanonischer Form (controllable canonical form) oder RKF.

SI-Systeme treten oft auf. Insbesondere die regelbar-kanonische Form erhält man direkt, wenn man eine DGL höheren Grades in ein System erster Ordnung umformt. Die Kalman-Matrix \(\widetilde {K}\) von \((\widetilde {A}, \widetilde {B})\) ist eine quadratische, obere Dreiecksmatrix \(\widetilde {K} = \smallpmatrix {1 & -\alpha _1 & \ast & \cdots & \ast \\ & 1 & -\alpha _1 & \cdots & \ast \\ & & \ddots & \ddots & \vdots \\ & & & 1 & -\alpha _1 \\ 0 & & & & 1}\) mit Einsen auf der Diagonalen. Daher ist sie für alle \(\alpha _1, \dotsc , \alpha _n \in \real \) invertierbar.

Lemma (RKF ist regelbar):
Jede regelbar-kanonische Form \((\widetilde {A}, \widetilde {B})\) ist regelbar.

Satz ( jedes regelbare SI-System kann in RKF gebracht werden):
Für jedes regelbare SI-System \(\dot {x} = Ax + Bu\) (also \(m = 1\)) gibt es eine Koordinatentransformation \(z = Tx\) mit \(T\) invertierbar, sodass \(\dot {z} = [TAT^{-1}] z + [TB] u\) in regelbar-kanonischer Form ist.

Der Beweis ist konstruktiv: Wenn \(s_1, \dotsc , s_n\) die Spalten von \(S = T^{-1} = \smallpmatrix {s_1 & \cdots & s_n}\) sind, dann muss \(B = S\widetilde {B}\) und \(AS = S\widetilde {A}\) mit \((\widetilde {A}, \widetilde {B})\) in RKF (siehe oben) gelten. Aus der ersten Gleichung erhält man \(s_1 := B\). Induktiv setzt man in die zweite Gleichung ein, um
\(s_2 := (A + \alpha _1 I) B\), \(s_3 := (A^2 + \alpha _1 A + \alpha _2 I) B\), …, \(s_n := (A^{n-1} + \alpha A^{n-1} + \dotsb + \alpha _{n-1} I) B\) zu erhalten. Etwas zusätzliche Argumentation ist noch nötig (z. B. warum \(S\) invertierbar ist).

Weil sich das charakteristische Polynom in der RKF sofort ablesen lässt (nämlich
\(\chi _{\widetilde {A}}(\lambda ) = \lambda ^n + \alpha _1 \lambda ^{n-1} + \dotsb + \alpha _n\)) und ähnliche Matrizen dasselbe charakteristische Polynom besitzen, lässt sich die regelbar-kanonische Form von \((A, B)\) direkt angeben und ist eindeutig.

Regelbarkeits-Normalform (MI-Systeme)

Im Folgenden geht es hauptsächlich um MI-Systeme, die Sätze lassen sich aber auch auf SI-Systeme anwenden.

MI-System: Ein MI-System (multi-input system) ist ein System \(\dot {x} = Ax + Bu\) mit \(m > 1\).

Unregelbarkeit: Unregelbarkeit kann viele Ursachen haben. Durch Verbindung von regelbaren System (Parallel-, Reihenschaltung, Rückführung) kann Regelbarkeit zerstört werden – muss aber nicht. Eine mögliche Situation tritt auf, wenn zwei identische regelbare Systeme \(\dot {x}_S = A_S x_S + B_S u\) mit demselben Eingang gesteuert werden, d. h. \(\dot {x} = Ax + Bu\) mit \(A := \smallpmatrix {A_S & 0 \\ 0 & A_S}\) und \(B := \smallpmatrix {B_S \\ B_S}\). Die Kalman-Matrix von \((A, B)\) hat keinen vollen Zeilenrang, weil sie gleich \(\smallpmatrix {B_S & A_S B_S & \cdots & A_S^{n-1} B_S \\ B_S & A_S B_S & \cdots & A_S^{n-1} B_S}\) ist. Die erreichbare Menge von \((A, B)\) ist gleich \(\left \{\left .\smallpmatrix {x \\ x} \;\right |\; x \in \real ^n\right \}\).

Herleitung der RNF: Falls \(\dot {x} = Ax + Bu\) nicht regelbar ist, dann gilt \(n_1 := \rg (K) < n\) bzw. \(n_2 := n - n_1 > 0\). Fasst man \(n_1\) linear unabhängige Spalten von \(K\) in der Matrix \(S_1 \in \real ^{n \times n_1}\) zusammen, so kann man diese mit \(n_2\) Vektoren, die in der Matrix \(S_2 \in \real ^{n \times n_2}\) zusammengefasst werden, zu einer Basis von \(\real ^n\) ergänzen. Die invertierbare Matrix \(S := \smallpmatrix {S_1 & S_2} \in \real ^{n \times (n_1 + n_2)}\) kann man zur Zustandskoordinaten-Transformation verwenden.

Struktur der RNF: Es gilt \(\widetilde {A} := S^{-1} AS = \smallpmatrix {A_{11} & A_{12} \\ 0 & A_{22}}\) und \(\widetilde {B} := S^{-1} B = \smallpmatrix {B_1 \\ 0}\) mit
\(A_{11} \in \real ^{n_1 \times n_1}\), \(A_{22} \in \real ^{n_2 \times n_2}\) und \(B_1 \in \real ^{n_1 \times m}\). Außerdem ist \((A_{11}, B_1)\) regelbar.

Satz (Regelbarkeits-Normalform): Für jedes lineare System \(\dot {x} = Ax + Bu\) gibt es eine Zustandskoordinaten-Transformation, die das System in das System
\(\smallpmatrix {\dot {z}_1 \\ \dot {z}_2} = \smallpmatrix {A_{11} & A_{12} \\ 0 & A_{22}} \smallpmatrix {z_1 \\ z_2} + \smallpmatrix {B_1 \\ 0} u\) transformiert, wobei \((A_{11}, B_1)\) regelbar ist.
Diese Form heißt Regelbarkeits-Normalform (controllability normal form) oder RNF.

Ausgeschrieben bedeutet das \(\dot {z}_1 = A_{11} z_1 + A_{12} z_2 + B_1 u\), \(\dot {z}_2 = A_{22} z_2\). Somit kann \(z_2(\cdot )\) nicht durch die Steuergröße beeinflusst werden.

unregelbare Eigenwerte:
Die Eigenwerte von \(A_{22}\) heißen unregelbare Eigenwerte (uncontrollable modes) von \((A, B)\).

Mit \(z_1(0) = z_1^0\) gilt \(z_1(t) = e^{A_{11}t} z_1^0 + \int _0^t e^{A_{11}(t - \tau )} \smallpmatrix {A_{12} & B_1} \smallpmatrix {z_2(\tau ) \\ u(\tau )} \d \tau \), wenn man \(z_2\) und \(u\) in einem Eingang zusammenfasst. Indem man \(z_2(t) = e^{A_{22}t} z_2^0\) (\(z_2(0) = z_2^0\)) einsetzt, erhält man die Lösung \(z_1(t) = e^{A_{11}t} \left (z_1^0 + \left [\int _0^t e^{-A_{11}\tau } A_{12} e^{A_{22}\tau } \d \tau \right ] z_2^0\right ) + \int _0^t e^{A_{11}(t - \tau )} B_1 u(\tau ) \d \tau \). Weil \((A_{11}, B_1)\) regelbar ist, kann man den Zustand \(z_1\) von jedem Anfangzustand \(z_1^0\) zur Zeit \(0\) in jeden Endzustand \(z_1^f\) zur Zeit \(T > 0\) regeln, wenn man von \(z_1^0\) vorher den „Störterm“ \([\cdots ]z_2^0\) abzieht.

Links-Eigenvektor:
\(e\) ist ein Links-Eigenvektor einer Matrix \(A\), falls \(e \not = 0\) und \(e^\ast (A - \lambda I) = 0\) mit \(e^\ast := \overline {e}^T\).

Satz (Hautus-Test zur Regelbarkeit): \((A, B)\) ist regelbar genau dann, wenn für jeden Links-Eigenvektor \(e\) von \(A\) gilt, dass \(e^\ast B \not = 0\). Äquivalent dazu ist, dass die Matrix \(\smallpmatrix {A - \lambda I & B}\) vollen Zeilenrang für alle \(\lambda \in \complex \) besitzt.

Wegen \(S^{-1} \smallpmatrix {A - \lambda I & B} \smallpmatrix {S & 0 \\ 0 & I} = \smallpmatrix {\widetilde {A} - \lambda I & \widetilde {B}}\) und \(\rg \smallpmatrix {A_{11} - \lambda I & B_1} = n_1\) (d. h. voller Zeilenrang) für alle \(\lambda \in \complex \) gilt \(\rg \smallpmatrix {A - \lambda I & B} = \rg \smallpmatrix {\widetilde {A} - \lambda I & \widetilde {B}} = n_1 + \rg (A_{22} - \lambda I)\) für alle \(\lambda \in \complex \), also folgendes Korollar, mit dem sich die unregelbaren Eigenwerte ohne Berechnung der RNF bestimmen lassen.

Folgerung: Die unregelbaren Eigenwerte von \((A, B)\) sind gegeben durch
\(\left \{\lambda \in \complex \;\left |\; \rg \smallpmatrix {A - \lambda I & B} < n\right .\right \}\).

Stabilisierbarkeit

Stabilisierbarkeit ist eine Verallgemeinerung von Regelbarkeit. Regelbarkeit von \(\dot {x} = Ax + Bu\) impliziert, dass jeder Anfangszustand in einem endlichen Zeitintervall zur \(0\) gesteuert werden kann (sogar in jedem beliebig kleinen Intervall). Bei Stabilisierbarkeit verlangt man dies nur noch asymptotisch für \(t \to \infty \).

Stabilisierbarkeit: Das lineare System \(\dot {x} = Ax + Bu\) (oder das Paar \((A, B)\)) heißt stabilisierbar (stabilizable), falls für jeden Anfangszustand \(\xi \in \real ^n\) eine stückweise stetige Steuergröße
\(u\colon [0, \infty ) \rightarrow \real ^m\) existiert, sodass \(\lim _{t \to \infty } x(t) = 0\) für \(x(0) = \xi \).

Jedes regelbare System ist stabilisierbar: Wähle \(T > 0\) beliebig. Wenn \(u_T(\cdot )\) die Steuergröße ist, die von \(x(0) = \xi \) zu \(x(T) = 0\) steuert, dann ist \(u(t) := u_T(t)\) für \(t \le T\) und \(u(t) := 0\) für \(t > T\) eine stabilisierende Steuergröße, da \(\dot {x} = Ax + Bu = 0\) für \(x = u = 0\), also \(x(t) = 0\) für \(t > T\).

Hautus-Test zur Stabilisierbarkeit: \((A, B)\) ist stabilisierbar genau dann, wenn die unregelbaren Eigenwerte alle negative Realteile besitzen. Äquivalent dazu ist, dass \(\smallpmatrix {A - \lambda I & B}\) vollen Zeilenrang für alle \(\lambda \in \complex \) mit \(\Re (\lambda ) \ge 0\) besitzt.

Dabei reicht es natürlich, nur die Eigenwerte \(\lambda \) von \(A\) mit nicht-negativem Realteil zu betrachten. Wenn \(A\) eine Hurwitz-Matrix ist, dann ist \(\dot {x} = Ax + Bu\) stabilisierbar (mit \(u(t) \equiv 0\)).

Offene und geschlossene Regelkreise

offene Regelkreise: Bisher wurden nur offene Regelkreise (open-loop control) betrachtet, die durch eine A-priori-Steuergröße \(u(t)\) für \(t \ge 0\) gesteuert werden. Das geregelte System wird durch \(\dot {x}(t) = Ax(t) + Bu(t)\) mit \(x(0) = \xi \) beschrieben. Dieser Ansatz besitzt einige Nachteile:

• Für verschiedene Anfangsbedingungen müssen verschiedene Steuergrößen gewählt werden, um die Aufgabenstellung zu erfüllen. Die Steuergrößen müssen „manuell“ an den jeweiligen Anfangszustand angepasst werden.

• Zukünftige, unvorhergesehene Ereignisse werden nicht berücksichtigt. Strategien mit offenen Regelkreisen sind vorgeplant und passen sich nicht Situationen an, in denen das System sich nicht gewünscht verhält, d. h. sie sind nicht robust.

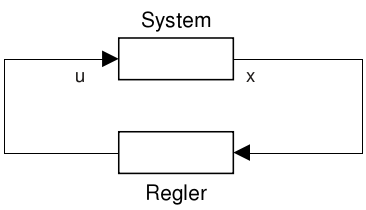
geschlossene Regelkreise (Rückführung): In einem geschlossenen Regelkreis empfängt ein Rückführungsregler (feedback controller) Informationen vom System, verarbeitet diese und erzeugt ein Steuersignal, das zurück zum System gesendet wird. Man kann dies wie folgt grafisch veranschaulichen:

Polvorgabe

Regelung durch lineare Zustandsrückführung: Bei einem System mit \(x\)-Dimension \(n\) und \(u\)-Dimension \(m\) ist der lineare Zustandsrückführungs-Regler (linear state-feedback controller) definiert durch \(u = -Fx\) mit \(F \in \real ^{m \times n}\).

Für ein LTI-System \(\dot {x} = Ax + Bu\) führt dies zu \(\dot {x} = Ax - BFx = (A - BF)x\) (geschlossener Regelkreis (closed-loop system) oder geregeltes System). Der Regler verändert daher die Dynamik des Systems vom ungeregelten System \(\dot {x} = Ax\) zum geregelten System \(\dot {x} = (A - BF)x\). Eine andere Interpretation ist, dass der Regler zur Zeit \(t\) den Zustand \(x(t)\) misst und die Steuergröße \(u(t) = -Fx(t)\) durch Bildung von Linearkombinationen der Einträge von \(x(t)\) berechnet.

Die Eigenwerte des Systems \(\dot {x} = (A - BF)x\) bestimmen das Verhalten des Systems. Umso erstaunlicher ist es, dass bei regelbaren Systemen die Matrix \(F\) stets so gewählt werden kann, dass \(A - BF\) beliebig vorgegebene Eigenwerte besitzt. Weil diese eine Obermenge der Polstellen der Übertragungsmatrix darstellen, spricht man auch von Polvorgabe (pole placement).

Satz (Polvorgabe): Sei \((A, B)\) regelbar mit \(A \in \real ^{n \times n}\) und \(B \in \real ^{n \times m}\).
Wenn \(\lambda _1, \dotsc , \lambda _n \in \complex \) (nicht notwendigerweise paarweise verschieden) symmetrisch bzgl. der reellen Achse sind, dann gibt es eine Matrix \(F \in \real ^{m \times n}\) mit \(\Eig (A - BF) = \{\lambda _1, \dotsc , \lambda _n\}\).

Beweis für SI-Systeme: Ist \(m = 1\), dann lässt sich \((A, B)\) in RKF bringen, d. h.
\(\widetilde {A} = \smallpmatrix {-\alpha _1 & -\alpha _2 & \cdots & -\alpha _n \\ 1 & 0 & & & \\ & \ddots & \ddots & & \\ 0 & & 1 & 0}\), \(\widetilde {B} = \smallpmatrix {1 \\ 0 \\ \vdots \\ 0}\) und \(\widetilde {A} - \widetilde {B} \widetilde {F} = \smallpmatrix {-\alpha _1 - \widetilde {f}_1 & -\alpha _2 - \widetilde {f}_2 & \cdots & -\alpha _n - \widetilde {f}_n \\ 1 & 0 & & & \\ & \ddots & \ddots & & \\ 0 & & 1 & 0}\)
mit \(\widetilde {A} = TAT^{-1}\) und \(\widetilde {B} = TB\) für \(T \in \GL _n(\real )\) und \(\widetilde {F} = \smallpmatrix {\widetilde {f}_1 & \cdots & \widetilde {f}_n} \in \real ^{1 \times n}\). Damit gilt
\(\chi _{\widetilde {A} - \widetilde {B} \widetilde {F}}(s) = s^n + (\alpha _1 + \widetilde {f}_1) s^{n-1} + \dotsb + (\alpha _n + \widetilde {f}_n)\). Durch Wahl von \(\widetilde {F}\) kann \(\chi _{\widetilde {A} - \widetilde {B} \widetilde {F}}\) jedes beliebige reelle, normierte Polynom \(n\)-ten Grades sein, also auch \((s - \lambda _1) \dotsm (s - \lambda _n)\). Für \(F := \widetilde {F} T\) gilt dann \(\widetilde {A} - \widetilde {B} \widetilde {F} = TAT^{-1} - TBFT^{-1} = T(A - BF)T^{-1}\), somit \(\chi _{A - BF} = \chi _{\widetilde {A} - \widetilde {B} \widetilde {F}}\).

Wenn man sich die Konstruktion von \(S = T^{-1}\) im Beweis zur regelbar-kanonischen Form anschaut, dann sieht man, dass \(S = K T_\alpha \) mit \(K := \smallpmatrix {B & AB & \cdots & A^{n-1} B}\) der Kalman-Matrix und \(T_\alpha := \smallpmatrix {1 & \alpha _1 & \alpha _2 & \cdots & \alpha _{n-1} \\ & 1 & \alpha _1 & \cdots & \alpha _{n-2} \\ & & 1 & \cdots & \alpha _{n-3} \\ & & & \ddots & \vdots \\ 0 & & & & 1}\). Daher muss man \(F = \smallpmatrix {\widetilde {f}_1 & \cdots & \widetilde {f}_n} [K T_\alpha ]^{-1}\) wählen, wenn das charakteristische Polynom von \(A - BF\) die Koeffizienten \(\alpha _1 + \widetilde {f}_1\), …, \(\alpha _n + \widetilde {f}_n\) haben soll (Bass-Gura-Formel oder alternative Ackermann-Formel).

Beweis für MI-Systeme: Für den Beweis für \(m > 1\) benötigt man zwei Lemmata.

Lemma: Für \((A, B)\) regelbar gibt es für alle \(b \in R(B) \setminus \{0\}\) Vektoren \(u_1, \dotsc , u_{n-1} \in \real ^m\), sodass \(\{x_1, \dotsc , x_n\}\) linear unabhängig ist, wobei die \(x_i\) definiert sind durch \(x_1 := b\) und die Rekursion \(x_{i+1} := Ax_i + Bu_i\), \(i = 1, \dotsc , n - 1\).

Der Beweis erfolgt per Induktion: Wegen \(x_1 = b \not = 0\) ist \(\{x_1\}\) l.u. Seien \(x_1, \dotsc , x_k\) l.u. mit \(k < n\) und \(V := [x_1, \dotsc , x_k]\). Zeige \(Ax_k + Bu_k \notin V\) für ein \(u_k \in \real ^m\) durch Widerspruch: Angenommen, für alle \(u \in \real ^m\) gilt \(Ax_k + Bu \in V\). Dann gilt insbesondere \(Ax_k \in V\) und somit \(Bu \in V\) für alle \(u \in \real ^m\), d. h. \(R(B) \subset V\). Damit gilt \(Ax_i = x_{i+1} - Bu_i \in V\) für alle \(i = 1, \dotsc , k - 1\), zusätzlich gilt \(Ax_k \in V\). \(V\) ist also \(A\)-invariant und enthält \(R(B)\), d. h. \(\real ^n = R(K) \subset V\) aufgrund \((A, B)\) regelbar, ein Widerspruch zu \(\dim V = k < n\).

Heymann-Lemma: Für \((A, B)\) regelbar gibt es für alle \(b \in R(B) \setminus \{0\}\) eine Matrix \(F \in \real ^{m \times n}\), sodass \((A + BF, b)\) regelbar ist.

Seien \(u_1, \dotsc , u_{n-1} \in \real ^m\) so gewählt, dass die \(x_1, \dotsc , x_n\) aus dem vorherigen Lemma linear unabhängig sind. Für \(u_n := 0\) sei \(F := \smallpmatrix {u_1 & \cdots & u_n} \cdot \smallpmatrix {x_1 & \cdots & x_n}^{-1}\). Dann ist \(Fx_i = u_i\) und somit \(x_{i+1} = Ax_i + Bu_i = (A + BF)x_i\) für \(i = 1, \dotsc , n - 1\). Man erhält also \(x_i = (A + BF)^{i-1} x_1 = (A + BF)^{i-1} b\) für \(i = 1, \dotsc , n\). Die Matrix \(\smallpmatrix {x_1 & \cdots & x_n}\) ist daher die Kalman-Matrix von \((A + BF, b)\), weil sie invertierbar ist (Spalten linear unabhängig), ist \((A + BF, b)\) regelbar.

Beweis für MI-Systeme: Mit dem Heymann-Lemma folgt der Satz über die Polvorgabe: Wähle \(b \in R(B) \setminus \{0\}\) (wenn \(B\) die Nullmatrix wäre, dann wäre \((A, B)\) nicht regelbar). Sei \(\widetilde {F} \in \real ^{m \times n}\) nach dem Heymann-Lemma, sodass \((A + B\widetilde {F}, b)\) regelbar ist. Wähle \(\widehat {F} \in \real ^{1 \times n}\), sodass \(\Eig ((A + B\widetilde {F}) - b\widehat {F}) = \{\lambda _1, \dotsc , \lambda _n\}\) (geht nach dem schon bewiesenen Fall \(m = 1\)). Wegen \(b \in R(B)\) gibt es \(u_0 \in \real ^m\) mit \(Bu_0 = b\). Definiere \(F := u_0 \widehat {F} - \widetilde {F}\). Damit gilt \(A - BF = A + B\widetilde {F} - Bu_0\widehat {F} = A + B\widetilde {F} - b\widehat {F}\), d. h. \(A - BF\) besitzt die gewünschten Eigenwerte.

unregelbare Systeme: Jedes System \((A, B)\) kann in Regelbarkeits-Normalform \((\widetilde {A}, \widetilde {B})\) gebracht werden. Wenn \(\widetilde {F}\) eine Rückführungsverstärkung für das transformierte System ist, dann können die Spalten von \(\widetilde {F} = \smallpmatrix {\widetilde {F}_1 & \widetilde {F}_2}\) wie die von \(\widetilde {A}\) eingeteilt werden. Mit \(u = -\widetilde {F}z\) erhält man das System \(\smallpmatrix {\dot {z}_1 \\ \dot {z}_2} = \smallpmatrix {A_{11} - B_1\widetilde {F}_1 & A_{12} - B_1 \widetilde {F}_2 \\ 0 & A_{22}} \smallpmatrix {z_1 \\ z_2}\). Weil \((A_{11}, B_1)\) regelbar ist, können die Eigenwerte von \(A_{11} - B_1\widetilde {F}_1\) durch geeignete Wahl von \(\widetilde {F}_1\) beliebig gewählt werden. Daher wählt man \(\widetilde {F}_1\) immer so, dass sie alle negativen Realteil haben. Die Eigenwerte von \(A_{22}\) kann man durch die lineare Zustandsregelung nicht beeinflussen, was die Bezeichnung „unregelbare Eigenwerte“ noch einmal rechtfertigt. Für \((A, B)\) unregelbar gibt es also immer Eigenwerte von \(A - BF\), die fest sind und nicht durch \(F\) verschoben werden können.

Satz (Stabilisierung durch lineare Zustandsrückführung): Das System \(\dot {x} = Ax + Bu\) ist stabilisierbar genau dann, wenn es eine Matrix \(F \in \real ^{m \times n}\) gibt, sodass \(\dot {x} = (A - BF)x\) asymptotisch stabil ist (d. h. \(A - BF\) ist eine Hurwitz-Matrix).

Zusatz: Kanonische Brunovsky-Form

äquivalent: Die Paare \((A, B)\) und \((\widetilde {A}, \widetilde {B})\) (mit \(A, \widetilde {A} \in \real ^{n \times n}\) und \(B, \widetilde {B} \in \real ^{n \times m}\)) heißen äquivalent, falls es Matrizen \(S \in \real ^{n \times n}\) invertierbar, \(U \in \real ^{m \times m}\) invertierbar und \(F \in \real ^{m \times n}\) gibt, sodass \(S^{-1} \smallpmatrix {A & B} \smallpmatrix {S & 0 \\ -F & U} = \smallpmatrix {\widetilde {A} & \widetilde {B}}\).

Man kann das auch schreiben als \(\widetilde {A} = S^{-1} AS - S^{-1} BF\) und \(\widetilde {B} = S^{-1} BU\). Äquivalent dazu kann man auch \(-F\) durch \(-FS\) ersetzen. Äquivalenz von Paaren \((A, B)\) ist eine Äquivalenzrelation auf der Menge \(\real ^{n \times n} \times \real ^{n \times m}\) der Paare \((A, B)\). \((\widetilde {A}, \widetilde {B})\) ist regelbar genau dann, wenn \((A, B)\) regelbar ist.

Spezialfälle:

• Zustandskoordinaten-Transformation (\(F = 0\), \(U = I\)): \(\widetilde {A} = S^{-1} AS\) und \(\widetilde {B} = S^{-1} B\)
  (zugehöriges System \(\dot {z} = S^{-1} ASz + S^{-1} Bu\))

• Eingangskoordinaten-Transformation (\(S = I\), \(F = 0\)): \(\widetilde {A} = A\) und \(\widetilde {B} = BU\)
  (zugehöriges System \(\dot {x} = Ax + BUv\) mit \(u = Uv\))

• lineare Zustandsrückführung, neuer Eingang (\(S = I\), \(U = I\)): \(\widetilde {A} = A - BF\) und \(\widetilde {B} = B\)
  (zugehöriges System \(\dot {x} = (A - BF)x + Bv\) mit \(u = -Fx + v\))

Äquivalenz als Gruppenoperation: Wegen \(\smallpmatrix {S_1 & 0 \\ -F_1 & U_1} \cdot \smallpmatrix {S_2 & 0 \\ -F_2 & U_2} = \smallpmatrix {S_3 & 0 \\ -F_3 & U_3}\) mit \(S_3 := S_1 S_2\) invertierbar, \(U_3 = U_1 U_2\) invertierbar und \(F_3 := F_1 S_2 + U_1 F_2\) ist die Menge \(G\) der Blockmatrizen \(\smallpmatrix {S & 0 \\ -F & U}\) mit \(S\) und \(U\) invertierbar eine Gruppe bzgl. der Multiplikation (man braucht zusätzlich noch \(\smallpmatrix {I & 0 \\ 0 & I} \in G\) und \(\smallpmatrix {S & 0 \\ -F & U}^{-1} = \smallpmatrix {S^{-1} & 0 \\ U^{-1}FS^{-1} & U^{-1}} \in G\)). Diese Gruppe definiert eine Gruppenoperation auf der Menge \(\real ^{n \times n} \times \real ^{n \times m}\) der Paare von Matrizen \((A, B)\):
\(\smallpmatrix {S & 0 \\ -F & U} \cdot (A, B) := (\widetilde {A}, \widetilde {B}) = (S^{-1} AS - S^{-1} BF, S^{-1} BU)\). Die Bahnen unter dieser Operation sind genau die Äquivalenzklassen der obigen Äquivalenz.

Satz (kanonische Brunovsky-Form): Sei \((A, B)\) regelbar, wobei \(B \in \real ^{n \times m}\) vollen Spaltenrang hat. Dann gibt es \(\kappa _1, \dotsc , \kappa _m \in \natural \) mit \(\kappa _1 \ge \dotsb \ge \kappa _m\) (Regelbarkeits-Indizes (controllability indices)), sodass \((A, B)\) zu \((\widetilde {A}, \widetilde {B})\) äquivalent ist mit

\begin{align*} \widetilde {A} = \smallpmatrix { 0 & 0 & \dotsb & 0 & & & & & 0 \\ 1 & 0 & & 0 & & & & & \\ & \ddots & \ddots & \vdots & & & & & \\ 0 & & 1 & 0 & & & & & \\ & & & & \ddots & & & & \\ & & & & & 0 & 0 & \dotsb & 0 \\ & & & & & 1 & 0 & & 0 \\ & & & & & & \ddots & \ddots & \vdots \\ 0 & & & & & 0 & & 1 & 0 },\quad \widetilde {B} = \smallpmatrix { 1 & & 0 \\ 0 & & \\ \vdots & & \\ 0 & & \\ & \ddots & \\ & & 1 \\ & & 0 \\ & & \vdots \\ 0 & & 0 }, \end{align*} wobei die Dimensionen der Kästchen \(\kappa _i \times \kappa _i\) bzw. \(\kappa _i \times 1\) sind (\(i = 1, \dotsc , m\)).
Diese Form heißt kanonische Brunovsky-Form (Brunovsky canonical form).

Falls \(B\) nicht vollen Spaltenrang hat, dann gibt es eine Eingangskoordinaten-Transformation \(Uv = u\) mit \(U\) invertierbar, sodass \(BU = \smallpmatrix {\widetilde {B}_1 & 0}\) gilt und \(\widetilde {B}_1\) vollen Spaltenrang hat. In diesem Fall ist \(Bu = BUv = \smallpmatrix {\widetilde {B}_1 & 0} \smallpmatrix {v_1 \\ v_2} = \widetilde {B}_1 v_1\), d. h. der Teil \(v_2\) des neuen Eingangs ist nicht relevant. Daher nimmt man in der Literatur oft oBdA an, dass \(B\) vollen Spaltenrang hat.

Brunovsky-Form ohne lineare Zustandsregelung:
Man kann obigen Satz auch ohne lineare Zustandsregelung formulieren (d. h. \(F = 0\)).
Es gibt eine Zustands- und Eingangskoordinaten-Transformation von \((A, B)\) in \((\widetilde {A}, \widetilde {B})\) mit

\begin{align*} \widetilde {A} = \smallpmatrix { \ast & \ast & \cdots & \ast & \cdots & \cdots & \cdots & \cdots & \ast \\ 1 & 0 & & 0 & & & & & \\ & \ddots & \ddots & \vdots & & & & & \\ 0 & & 1 & 0 & & & & & \\ & & & & \ddots & & & & \\ \ast & \cdots & \cdots & \cdots & \cdots & \ast & \ast & \cdots & \ast \\ & & & & & 1 & 0 & & 0 \\ & & & & & & \ddots & \ddots & \vdots \\ 0 & & & & & 0 & & 1 & 0 },\quad \widetilde {B} = \smallpmatrix { 1 & & 0 \\ 0 & & \\ \vdots & & \\ 0 & & \\ & \ddots & \\ & & 1 \\ & & 0 \\ & & \vdots \\ 0 & & 0 }. \end{align*}

Polvorgabe mit kanonischer Brunovsky-Form: Mit der kanonischen Brunovsky-Form ist der Satz über die Polvorgabe einfach zu zeigen (allerdings ist der Satz über die kanonische Brunovsky-Form relativ aufwendig zu beweisen): Für \(\widetilde {F} \in \real ^{m \times n}\) beliebig ist \(\widetilde {B}\widetilde {F}\) eine \((n \times n)\)-Matrix, die nur Nullen enthält, außer in den \(\ast \)-Zeilen von \(\widetilde {A}\) (dort stehen die Zeilen von \(\widetilde {F}\)). Somit kann man die Elemente von \(\widetilde {F}\), die zu Einträgen von \(\widetilde {A}\) außerhalb von Blöcken gehören, so wählen, dass die \(\ast \)-Zeilen außerhalb der Blöcke \(\widetilde {A}_i\) verschwinden. Die übrigen Einträge von \(\widetilde {F}\) (in den Blöcken \(\widetilde {F}_i\)) wählt man so, dass \(\widetilde {A}_i - \widetilde {B}_i \widetilde {F}_i\) die gewünschten Eigenwerte besitzt, was aufgrund der Polvorgabe für SI-Systeme möglich ist. Damit besitzt auch \(\widetilde {A} - \widetilde {B} \widetilde {F}\) die gewünschten Eigenwerte. Wegen
\(\widetilde {A} - \widetilde {B} \widetilde {F} = S^{-1}AS - S^{-1}BF - S^{-1}BU \widetilde {F} = S^{-1}AS - S^{-1}B(F + U\widetilde {F}) = S^{-1} (A - B\widehat {F}) S\) mit \(\widehat {F} := (F + U\widetilde {F}) S^{-1}\) besitzt auch \(A - B\widehat {F}\) die geforderten Eigenwerte.

Dominante Eigenwerte

Dämpfungsverhältnis: Das Dämpfungsverhältnis (damping ratio) des nicht-reellen Eigenwerts \(\lambda \in \Eig (A) \setminus \real \) von \(A\) ist definiert als \(\zeta := -\frac {\Re (\lambda )}{|\lambda |}\).

dominanter Eigenwert: Ein Paar von nicht-reellen Eigenwerten \(\lambda , \overline {\lambda } \in \Eig (A) \setminus \real \) von \(A\) heißt dominant, falls ihr Dämpfungsverhältnis das kleinste aller Dämpfungsverhältnisse von nicht-reellen Eigenwerten von \(A\) ist.

Für Hurwitz-Matrizen \(A\) ist das Verhalten von \(t \mapsto e^{At}\) häufig (aber nicht immer) hauptsächlich bestimmt durch den dominanten Eigenwert von \(A\). Wegen der reellen Jordan-Normalform von \(A\) ist \(e^{At}\) eine Überlagerung von \(e\)-Funktionen mit reellen Exponenten oder von \(e^{Jt}\) mit \((2 \times 2)\)-Blöcken \(J\) mit nicht-reellen Eigenwerten. Ist ein solcher Block \(J\) eine Hurwitz-Matrix, dann bestimmt das Dämpfungsverhältnis die Dominanz der Antwort.

Platzierung der Eigenwerte: Diese Frage ist nicht leicht zu beantworten.

• Die Bass-Gura-Formel \(F = \smallpmatrix {\widetilde {f}_1 & \cdots & \widetilde {f}_n} [K T_\alpha ]^{-1}\) zeigt: Je kleiner die Verschiebung der Koeffizienten des charakteristischen Polynoms (und der Eigenwerte) ist, desto kleiner sind die Koeffizienten von \(F\) – was wünschenswert ist, denn große Koeffizienten bedeuten einen großen Regelaufwand.

• Die Rolle von dominanten Eigenwerten führt zum folgenden Design-Rezept:

  • Wähle ein System zweiter Ordnung mit der gewünschten Dynamik.

  • Platziere zwei Eigenwerte an den zwei Polstellen des Systems.

  • Wähle alle anderen Eigenwerte schneller (damit sie weniger dominant sind), aber nicht zu schnell (um zu starken Regelaufwand zu vermeiden).

  • Platziere die Eigenwerte und überprüfe mittels dynamischer Simulation.

  Üblicherweise muss man diesen Vorgang mehrmals wiederholen, um gute Ergebnisse zu erzielen.