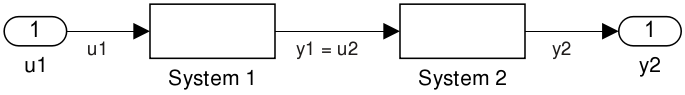Was ist Kontrolltheorie?
Rückführung (feedback): Bei dynamischen Systemen ändern sich die Variablen im Lauf der Zeit, oft durch externe Einflüsse. Bei einer sog. Rückführung (feedback) sind mehrere dynamische Systeme miteinander verbunden und beeinflussen sich gegenseitig.
Beispiele:
Knopf zur automatischen Geschwindigkeitsreglung in US-amerikanischen Autos
Biologie: z. B. die Regulierung des Glukosespiegels im Blut, damit dieser konstant bleibt (Leber und Pankreas messen bzw. schütten die Hormone Insulin und Glukagon aus und beeinflussen sich somit gegenseitig)
Steuerproblem: Flug einer Rakete zum Mond mit möglichst wenig Treibstoffaufwand
Fliehkraftregler (centrifugal governor): Dieser hält die Rotationsgeschwindigkeit auf einem konstanten Wert, der von der Belastung der Maschine unabhängig ist. Obwohl er seit dem 17. Jahrhundert bekannt ist, wird er meist Watt/Boulton (1788) zugeschrieben. Eine theoretische Stabilitätsanalyse wurde von Maxwell und Hurwitz durchgeführt. Man spricht von negativer Rückführung, da das Ventil geschlossen/geöffnet wird, wenn sich die Maschine zu schnell/zu langsam bewegt. Allerdings muss nicht ein stabiles Gleichgewicht eintreten, es wäre z. B. auch eine Oszillation möglich (wie die Temperatur beim Thermostat).
positive Auswirkungen von Rückführung:
Erhöhung der Unempfindlichkeit des Systems auf externe Einflüsse
(mehr Glukose durch Essen, Änderung der Belastung beim Fliehkraftregler)Erhöhung der Robustheit gegen Veränderungen in den Komponenten
(Veränderung der Masse des Rades beim Fliehkraftregler)lineares Verhalten bei nicht-linearen Systemen erzwingen
(Autopilot bei Kampfjets, Leistungselektronik)
negative Auswirkungen von Rückführung:
Erzeugung von dynamischen Instabilitäten, also Oszillationen oder bestimmte Divergenz
(Reduktion der Reibung durch Optimierung der Maschine kann zu Oszillationen beim Fliehkraftregler führen)Erhöhung der Empfindlichkeit auf externe Einflüsse und Veränderungen der Komponenten
(Verstärkung des Rauschens bei einem Sensor)
Kontrolltheorie: Der Zweck von Regelung (control) ist die Gestaltung von Komponenten eines technischen Rückführungssystems, um ein
gewünschtes Gesamtverhalten zu erzielen.
Kontrolltheorie (control theory) stellt die notwendigen mathematischen Grundlagen, Werkzeuge und Algorithmen sowie das nötige Vokabular bzw. die Technik bereit, um
dieses Ziel zu erreichen.
Mathematische Modelle dynamischer Systeme
dynamisches System:
In einem dynamischen System treten die Auswirkungen einer Aktion nicht sofort auf.
Zum Beispiel erhöht die Betätigung des Gaspedals im Auto nicht sofort die Geschwindigkeit, die Temperatur steigt nicht sofort an, wenn die Heizung angeschaltet wird, Kopfschmerzen verschwinden erst langsam, nachdem Medizin eingenommen wurde, und eine Geldanlage führt nur in der Zukunft zu Gewinnen oder Verlusten.
Variablen eines dynamischen Systems verändern sich mit der Zeit. Die Entwicklung hängt dabei von der äußeren Anregung ab, die sich selbst mit der Zeit ändert.
mathematisches Modell: Eine Möglichkeit der Analyse des Verhalten eines dynamischen Systems besteht mittels eines mathematischen Modells. Solche Modelle werden oft durch (gewöhnliche oder partielle) Differentialgleichungen beschrieben.
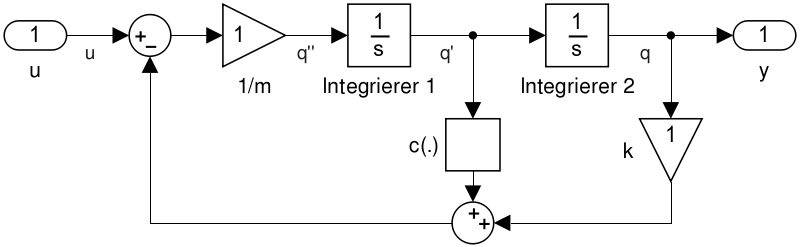
Beispiel: Beim gedämpften Federpendel (mass-spring-damper system) hängt eine Masse \(m\) mittels einer Feder (Federkonstante \(k\)) an einer Wand (Abstand \(q\), abhängig von der Zeit \(t\)). Gleichzeitig ist zwischen Masse und Wand eine Dämpfung \(c(\dot {q})\) eingebaut, die von der Geschwindigkeit der Masse abhängt (auch nicht-linear möglich). Nach dem zweiten Newtonschen Gesetz und dem Hookeschen Gesetz gilt \(m \ddot {q} + c(\dot {q}) + kq = 0\) (Federkraft wirkt in Richtung der Ruheposition).
Eingangsgrößen: Ein dynamisches System ist autonom (autonomous), falls es nicht externen Einflüssen ausgesetzt ist. Nicht-autonome Systeme haben externe Eingangsgrößen (inputs).
Beispiel: Im obigen Beispiel erhält man mit \(u(\cdot )\) der externen Kraft, die auf die Masse wirkt, \(m \ddot {q} + c(\dot {q}) + kq = u\). Die Kraft \(u(\cdot )\) variiert normalerweise mit der Zeit. Je nach Umständen kann sie auf zwei verschiedene Arten interpretiert werden:
Steuergröße (control input): falls \(u(\cdot )\) frei verändert werden darf
Störgröße (disturbance input): falls \(u(\cdot )\) durch die Natur feststeht und nicht verändert werden darf
Ausgangsgrößen: Meistens interessiert man sich nicht für alle Variablen, die in einem Modell vorkommen. Ausgangsgrößen (outputs) beschreiben die Größen, für die man sich interessiert.
Beispiel: Wenn man sich im obigen Beispiel nur für die Auslenkung interessiert, dann ist der Ausgang \(y\) bestimmt durch \(m \ddot {q} + c(\dot {q}) + kq = u\), \(y = q\). Für eine bestimmte Steuergröße \(u(\cdot )\) ist die Ausgangsgröße \(y(\cdot )\) eine Funktion in Abhängigkeit von der Zeit. Auch \(y\) kann auf zwei Arten interpretiert werden:
\(y\) ist eine Variable, die gemessen werden kann (mittels Sensoren).
\(y\) ist eine Variable, die zur Analyse der Eigenschaften des Systems überwacht werden soll (in der Simulation).
Interpretation des Modells: Seien \(u(t)\) eine Eingangsgröße, die für \(t \ge 0\) definiert ist, und \(q_0\) und \(v_0\) eine Anfangsposition bzw. eine Anfangsgeschwindigkeit. Falls \(u \in \C \) und \(c \in \C ^1\) gilt, dann hat das Anfangswertproblem \(m \ddot {q}(t) + c(\dot {q}(t)) + k q(t) = u(t)\) mit \(q(0) = q_0\), \(\dot {q}(0) = v_0\) eine eindeutige, differenzierbare Lösung \(q(t)\), die für \(t \in [0, t_1)\) mit einem \(t_1 > 0\) definiert ist (die Lösung muss nicht für alle \(t \ge 0\) existieren).
Zustandsgröße: Weil die Werte für \(q(0)\) und \(\dot {q}(0)\) die Lösung der DGL (für eine feste Eingangsgröße) eindeutig festlegen, heißen \(x = \smallpmatrix {x_1 \\ x_2} := \smallpmatrix {q \\ \dot {q}}\) und \(x(t) = \smallpmatrix {x_1(t) \\ x_2(t)} := \smallpmatrix {q(t) \\ \dot {q}(t)}\) Zustandsvektor (state-vector) bzw. Zustandsgröße (state-response). Der Ausgang (response) des Systems ist bestimmt durch \(y(t) = q(t)\).
Verhalten: Bei einem System wie \(m \ddot {q} + c(\dot {q}) + kq = u\), \(y = q\) ist man an seinem Verhalten (behavior) interessiert, also die Menge aller Eingangs-, Zustands- und Ausgangsgrößen \(u(\cdot )\), \((q(\cdot ), \dot {q}(\cdot ))\) und \(y(\cdot )\), die diese Gleichung erfüllen.
Trajektorien: Signale (signals) oder Traktorien (trajectories) sind vektorwertige Funktionen der Zeit. Normalerweise wird stillschweigend angenommen, dass sie abschnittsweise stetig sind.
Die Bedingungen, die erfüllt sein müssen, werden oft durch DGLs beschrieben. Dabei müssen Annahmen gemacht werden, sodass die Existenz und Eindeutigkeit der Lösung des Anfangswertproblems sichergestellt ist.
Äquivalenz: Verschiedene Beschreibungen eines Systems können zum selben Verhalten führen. In diesem Fall heißen die System(-Beschreibungen) äquivalent (equivalent). Im sog. verhaltensbasierten Ansatz bei dynamischen Systemen wird die nötige Theorie in einer mathematisch präzisen Weise entwickelt.
beispielhafte Fragen:
Falls es keinen externen Einfluss gibt, wie verhalten sich die Zustands- und Ausgangsgröße?
Kann das System von einer Position in eine andere gebracht werden (Steuerproblem, steering problem)?
Ist es möglich, die Eingangs- aus der Ausgangsgröße zu rekonstruieren?
Kann das System so modifiziert werden, sodass ein gewünschtes Verhalten erzielt wird?
Bei manchen von diesen (groben) Fragen muss das System auf seine Eigenschaften hin untersucht werden, bei anderen müssen Eingangsgrößen verarbeitet oder die Systembedingungen verändert werden, um das Verhalten des Systems zu ändern. Mit der Kontrolltheorie versucht man, solche Fragen systematisch zu beantworten.
von Modellen zweiter zu Modellen erster Ordnung: Die Beschreibung \(m \ddot {q} + c(\dot {q}) + kq = u\) beinhaltet die ersten beiden Ableitungen von \(q\). Für \(m \not = 0\) heißt sie DGL zweiter Ordnung. Mit den Zustandsvariablen (state-variables) \(x_1 = q\) und \(x_2 = \dot {q}\) gilt \(\dot {x}_1 = \dot {q} =
x_2\), also
\(\dot {x}_2 = \ddot {q} = -\frac {k}{m} q - \frac {c(\dot {q})}{m} + \frac {1}{m} u = -\frac {k}{m} x_1 - \frac {1}{m} c(x_2) + \frac {1}{m} u\). Das kann geschrieben werden als
\(\dot {x} := \smallpmatrix {\dot {x}_1 \\ \dot {x}_2} = \smallpmatrix {x_2 \\ -\frac {k}{m} x_1 - \frac {1}{m} c(x_2) + \frac {1}{m} u} =: f(x, u)\), man erhält also eine zweidim.
DGL erster Ordnung.
Lemma (Umwandlung in System erster Ordnung): Sei \(r\) eine reellwertige, nicht-lineare Funktion mit \(n + 1\) Argumenten. Dann ist das System \(q^{(n)} + r(q^{(n-1)}, q^{(n-2)}, \dotsc , \dot {q}, q, u) = 0\) äquivalent zu \(\dot {x} := \smallpmatrix {\dot {x}_1 \\ \dot {x}_2 \\ \vdots \\ \dot {x}_{n-1} \\ \dot {x}_n} = \smallpmatrix {x_2 \\ x_3 \\ \vdots \\ x_n \\ -r(x_n, x_{n-1}, \dotsc , x_2, x_1, u)} =: f(x, u)\).
Diese Methode ist jedoch nicht eindeutig:
Lemma (Umwandlung in System erster Ordnung 2): Sei \(r\) eine reellwertige, nicht-lineare Funktion mit \(n + 1\) Argumenten. Dann ist das System \(q^{(n)} + r(q^{(n-1)}, q^{(n-2)}, \dotsc , \dot {q}, q, u) = 0\) äquivalent zu \(\dot {z} := \smallpmatrix {\dot {z}_1 \\ \dot {z}_2 \\ \vdots \\ \dot {z}_{n-1} \\ \dot {z}_n} = \smallpmatrix {-r(z_1, z_2, \dotsc , z_{n-1}, z_n, u) \\ z_1 \\ \vdots \\ z_{n-2} \\ z_{n-1}} =: \widehat {f}(z, u)\).
Zustandsraum-Darstellung: Physikalische Modelle führen oft zu einem System von DGLs höherer Ordnung. Wie gerade gezeigt, können diese oft (aber nicht immer!) äquivalent
geschrieben werden als eine Vektor-DGL erster Ordnung \(\dot {x} = f(x, u)\) und \(y = h(x, u)\) mit Abbildungen \(f\colon X \times U \rightarrow \real ^n\) und \(h\colon X \times U \rightarrow \real ^k\),
wobei \(X \subset \real ^n\) und \(U \subset \real ^m\).
Ausführlich geschrieben:
\begin{align*} \dot {x}_1 &= f_1(x_1, \dotsc , x_n, u_1, \dotsc , u_m),& y_1 &= h_1(x_1, \dotsc , x_n, u_1, \dotsc , u_m),\\ &\;\;\vdots &&\;\;\vdots \\ \dot {x}_n &= f_n(x_1, \dotsc , x_n, u_1, \dotsc , u_m),& y_k &= h_k(x_1, \dotsc , x_n, u_1, \dotsc , u_m). \end{align*} Diese Darstellung nennt man die Zustandsraum-Darstellung (state-space description). Die Funktionen können auch explizit von der Zeit abhängen.
Wenn \(u(\cdot )\colon I \rightarrow U\) eine Eingangsgröße auf einem offenen Intervall \(I \subset \real \) mit \(0 \in I\) und \(\xi \in \real ^n\) eine Anfangsbedingung für den Zustand ist, dann erhält man die Zustandsgröße durch Lösung des AWP \(\dot {x}(t) = f(x(t), u(t))\), \(x(0) = \xi \). Die Ausgangsgröße ist dann einfach \(y(t) := h(x(t), u(t))\) für \(t \in I\).
Die Existenz und Eindeutigkeit der Zustandsgröße \(x\) auf einem offenen Teilintervall von \(I\) ist garantiert, wenn \(f\) stetig in \((x, u)\), \(f\) Lipschitz-stetig in \(x\) und \(u\) stetig ist. Das gilt auch für Eingänge \(u\), die nur abschnittsweise stetig sind (endlich viele Sprungstellen). In diesem Fall löst man die DGL abschnittsweise und setzt als Anfangsbedingung für den zweiten Abschnitt den Wert der Lösung im ersten Abschnitt an der Zeit ein, an der der Sprung stattfindet. Dadurch ist die Lösung in jedem Fall stetig, wird jedoch Sprünge in der Ableitung besitzen.
allgemeine Beschreibung eines linearen Systems: Wenn \(f\) und \(h\) linear sind, dann gilt \(f(x, u) = Ax + Bu\) und \(h(x, u) = Cx + Du\) mit \(A \in \real ^{n \times n}\), \(B \in \real ^{n \times
m}\), \(C \in \real ^{k \times n}\), \(D \in \real ^{k \times m}\).
Daher wird ein allgemeines lineares, zeit-invariantes System, genannt LTI-System (linear, time-
invariant system), beschrieben durch \(\dot {x} = Ax + Bu\), \(y = Cx + Du\).
Dieses System wird im Folgenden hauptsächlich verwendet, denn viele technische Systeme können oft durch lineare Systeme angenähert werden. Andererseits benötigen physikalische Modelle oft nicht-lineare dynamische Systeme.
Wiederholung: Globale Existenz und Eindeutigkeit von Lösungen von Anfangswertproblemen
Sei das Anfangswertproblem \(\dot {x} = g(t, x)\), \(x(\tau ) = \xi \), für \(g\colon D \rightarrow \real ^n\) mit \(D \subset \real \times \real ^n\) gegeben.
Voraussetzungen: Seien \(D \subset \real \times \real ^n\) offen und \(g\colon D \rightarrow \real ^n\) stetig in \((t, x)\) und
lokal Lipschitz-stetig in \(x\), d. h. für alle \((\tau , \xi ) \in D\) gibt es eine Umgebung \(U \subset D\) von \((\tau ,
\xi )\) und ein \(L > 0\) mit \(\norm {g(t, x) - g(t, y)} \le L \norm {x - y}\) für alle \((t, x), (t, y) \in U\).
Die Voraussetzungen sind erfüllt, wenn \(g\) und \(\partial _x g\) stetig auf \(D\) sind, also insbesondere, wenn \(g \in \C ^1(D, \real ^n)\).
Satz (globale Existenz und Eindeutigkeit): Unter obigen Voraussetzungen gibt es für jedes \((\tau , \xi ) \in D\) ein maximales Existenzintervall \(I_{(\tau , \xi )} = (t_-, t_+)\) mit \(\tau \in
I_{(\tau , \xi )}\) und eine eindeutige \(\C ^1\)-Lösung \(x(\cdot , \tau , \xi )\colon I_{(\tau , \xi )} \rightarrow \real ^n\) des AWP \(\dot {x} = g(t, x)\), \(x(\tau ) = \xi \).
Maximalität von \(I_{(\tau , \xi )}\) bedeutet, dass für jede \(\C ^1\)-Lösung \(x_J\colon J \rightarrow \real ^n\) des AWP auf einem Intervall \(J\) mit \(\tau \in J\) automatisch \(J
\subset I_{(\tau , \xi )}\) und \(x_J = x|_J\) erfüllt ist.
Außerdem gilt für \(t_+ < \infty \) genau eine der folgenden beiden Eigenschaften (analog für \(t_- > -\infty \)):
Die Lösung divergiert bestimmt in der Norm:
\(\lim _{t \to t_+-0} \norm {x(t)} = \infty \).Die Lösung nähert sich dem Rand von \(D\) an:
Für alle Folgen \((t_\nu )_{\nu \in \natural }\) in \(I_{(\tau , \xi )}\) mit \(t_\nu \to t_+\) und \(x(t_\nu ) \to x_+\) gilt \((t_+, x_+) \in \partial D\).
Simulation
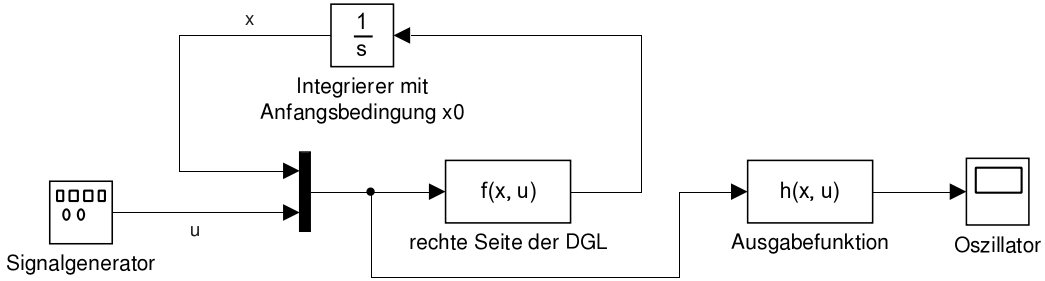
Integraldarstellung von DGLs: Die Beschreibung eines Systems mit Differential- und Ausgangsgleichung \(\dot {x}(t) = f(x(t), u(t))\), \(x(0) = \xi \), und \(y(t) = h(x(t), u(t))\) erlaubt die numerische Berechnung des Ausgangs (für einen Eingang und eine Anfangsbedingung) durch ODE-Löser wie z. B. ode45 oder ode15s in MATLAB. Durch Integration der DGL über die Zeit erhält man die Integraldarstellung \(x(t) = \xi + \int _0^t f(x(\tau ), u(\tau ))\d \tau \), \(y(t) = h(x(t), u(t))\).Die Darstellung kann man wie folgt interpretieren: Definiere zunächst die Abbildung \(\Sigma _1\) mit \(\smallpmatrix {x(\cdot ) \\ u(\cdot )} \mapsto z(\cdot )\), wobei \(z(t) := f(x(t), u(t))\) (statisches System (static system)). Definiere dann die Integration mit Anfangswert \(\xi \): \(\Sigma _2\) mit \(v(\cdot ) \mapsto w(\cdot )\), wobei \(w(t) := \xi + \int _0^t v(\tau )\d \tau \). Durch Komposition der beiden Abbildungen erhält man die Abbildung \(\Sigma _2 \circ \Sigma _1\) mit \(\smallpmatrix {x(\cdot ) \\ u(\cdot )} \mapsto w(\cdot )\), wobei \(w(t) := \xi + \int _0^t f(x(\tau ), u(\tau ))\d \tau \). Für ein festes \(u(\cdot )\) ist nun ein Fixpunkt \(x(\cdot )\) dieser Abbildung gesucht. Dies kann man in einem Simulink-Diagramm darstellen:
Den Ausgang erhält man dann einfach durch Anwendung von \(h(\cdot , \cdot )\) auf \(x(\cdot )\) und \(u(\cdot )\) (wie bei \(\Sigma _1\)).
inverses Pendel: Ein inverses Pendel (cart-pendulum system) ist ein mathematisches Pendel, das in der Ruhelage nach oben zeigt. Das Pendel kann nur in einer Dimension schwingen und ist auf einem Wagen befestigt, der sich in derselben Dimension hin- und her bewegen kann. Der „Wagen“ ist so gebaut, dass das Pendel auch nach unten schwingen kann, es kann also die 360° voll ausnutzen. Das Ziel ist, das Pendel durch Bewegung des Wagens in seiner instabilen Ruhelage zu halten. Ein Segway kann vereinfacht als inverses Pendel betrachtet werden.
Bezeichnet man die Masse am Pendel mit \(m\), die Masse des Wagens mit \(M\), die zurückgelegte Strecke des Wagens mit \(p\), die auf den Wagen wirkende Kraft mit \(F\), die Länge des Pendels mit \(\ell
\) und den Winkel der Auslenkung des Pendels aus der Ruhelage mit \(\theta \), so erhält man mit den Lagrange-Gleichungen \((M +
m)\ddot {p} - m\ell \cos (\theta )\ddot {\theta } + c\dot {p} + m\ell \sin (\theta )\dot {\theta }^2 = F\) sowie
\(-m\ell \cos (\theta )\ddot {p} + m\ell ^2\ddot {\theta } + \gamma \dot {\theta } - mg\ell \sin (\theta ) = 0\), wobei \(c\) und \(\gamma \) den Reibungswiderstand des Wagens und des Pendels
beschreiben.
Mit \(U(\theta ) := \smallpmatrix {M + m&-m\ell \cos (\theta )\\-m\ell \cos (\theta )&m\ell ^2}\) und \(v(\theta , \dot {p}, \dot {\theta }) := \smallpmatrix {c\dot {p} + m\ell \sin
(\theta )\dot {\theta }^2 \\ \gamma \dot {\theta } - mg\ell \sin (\theta )}\) kann man das System schreiben als \(U(\theta ) \smallpmatrix {\ddot {p} \\ \ddot {\theta }} + v(\theta , \dot {p}, \dot
{\theta }) = \smallpmatrix {F \\ 0}\). Dabei ist \(U(\theta )\) invertierbar, weil die Determinante für kein \(\theta \) verschwindet. Deswegen kann man dies schreiben als
\(\smallpmatrix {\ddot {p} \\ \ddot {\theta }} = -U(\theta )^{-1} v(\theta , \dot {p}, \dot {\theta }) + U(\theta )^{-1} \smallpmatrix {F \\ 0} =: \smallpmatrix {w_1(p, \theta , \dot {p},
\dot {\theta }, F) \\ w_2(p, \theta , \dot {p}, \dot {\theta }, F)}\).
Wenn man die Zustandsgrößen \(\smallpmatrix {x_1 \\ x_2} := \smallpmatrix {p \\ \theta }\) und \(\smallpmatrix {x_3 \\ x_4} := \smallpmatrix {\dot {p} \\ \dot {\theta }}\) sowie die Eingangsgröße \(u := F\) definiert, so kann das System durch \(\dot {x} = f(x, u)\) als System erster Ordnung beschrieben werden, wobei \(f(x, u) := \smallpmatrix {x_3 \\ x_4 \\ w_1(x, u) \\ w_2(x, u)}\).
Gleichgewichte und Linearisierung
Gleichgewicht: Alle Paare von Vektoren \((x_e, u_e) \in X \times U\) mit \(f(x_e, u_e) = 0\) heißen
Gleichgewichte (equilibria) des Systems \(\dot {x} = f(x, u)\).
Wenn ein System mit der konstanten Steuergröße \(u(t) = u_e\) betrieben wird, der Zustand durch \(x_e(t_0) = x_e\) initialisiert wird und die Lösung des Systems eindeutig ist, dann gilt \(x(t) \equiv x_e\) für alle \(t \ge t_0\) (weil das eine Lösung ist, da \(f(x_e, u_e) = 0\)).
Beispiel: Für Gleichgewichte in obiger DGL müssen die Ableitungen von \(p\) und \(\theta \) verschwinden, also \(0 = F\) und \(-mg\ell \sin (\theta ) = 0\). Die Lösungen sind \(\theta _e = 0\) (aufrechte Position) und \(\theta _e = \pi \) (nach unten zeigend), wobei \(p_e\) beliebig ist.
Herleitung der Linearisierung: Falls \(f\) und \(h\) stetig differenzierbar sind, kann man die Taylorentwicklungen erster Ordnung um \((x_e, u_e)\) berechnen als
\(f(x, u) \approx f(x_e, u_e) + \partial _x f(x_e, u_e) (x - x_e) + \partial _u f(x_e, u_e) (u - u_e)\) und
\(h(x, u) \approx y_e + \partial _x h(x_e, u_e) (x - x_e) + \partial _u h(x_e, u_e) (u - u_e)\), wobei \(y_e := h(x_e, u_e)\).
Dabei sind die partiellen Ableitungen die Jacobi-Matrizen. Die Näherung ist besonders gut, falls \(x \approx x_e\) und \(u \approx u_e\). Daher kann man die Entwicklungen zur Linearisierung von nicht-linearen
Systemen verwenden.
Linearisierung: Seien \(f(x_e, u_e) = 0\) und \(f, h \in \C ^1\). Dann ist die Linearisierung (linearization) von \(\dot {x} = f(x, u)\), \(y = h(x, u)\) bei \((x_e, u_e)\) gegeben durch \(\dot {x}_\Delta = A x_\Delta + B u_\Delta \), \(y_\Delta = C x_\Delta , + D u_\Delta \), wobei \(A := \partial _x f(x_e, u_e)\), \(B := \partial _u f(x_e, u_e)\), \(C := \partial _x h(x_e, u_e)\), \(D := \partial _u h(x_e, u_e)\).
Für die betrachteten \(t\) gelte \(u(t) \approx u_e\) und \(x(t) \approx x_e\). Für die nicht-lineare Ausgangsgröße gilt also \(y(t) \approx y_e\). Wenn man nun die Linearisierung mit
\(u_\Delta := u(t) - u_e\) für den Anfangswert \(x_\Delta (0) := x(0) - x_e\) ausführt, so hofft man, dass \(y_e + y_\Delta (t)\) die nicht-lineare Ausgangsgröße \(y(t)\) gut
approximiert.
Es gilt nämlich \(\left [x(t) - x_e\right ]^\cdot = \dot {x}(t) = f(x(t), u(t)) \approx A[x(t) - x_e] + Bu_\Delta (t)\) nach Definition der Linearisierung (\((x_e, u_e)\) ist nämlich ein
Gleichgewicht). Wenn die Trajektorie \(x(\cdot )\) nahe an \(x_e\) bleibt, dann ist die Taylor-Abschätzung besonders gut – würde ein Gleichheitszeichen stehen, dann wäre \([x(t) - x_e]\)
ebenfalls eine Lösung der Linearisierung, es müsste also \(x_\Delta (t) = x(t) - x_e\) gelten. Aufgrund der nur ungefähren Gleichheit gilt aber nur \(x_\Delta (t) \approx x(t) - x_e\).
Außerdem gilt \(\left [y(t) - y_e\right ] = h(x(t), u(t)) - y_e \approx C[x(t) - x_e] + Du_\Delta (t)\). Für \(x_\Delta (t) \approx x(t) - x_e\) ist die rechte Seite ungefähr gleich
\(y_\Delta (t)\), also \(y_\Delta (t) \approx y(t) - y_e\). So erhält man \(y(t) \approx y_e + y_\Delta (t)\).
Beispiel: Man betrachtet das inverse Pendel im nach unten zeigenden, stabilen Gleichgewicht. Wenn man nur kurz eine Kraft anwendet, dann schlägt das Pendel nur kurz in beide Richtungen aus, ehe es sich wieder
im Gleichgewicht befindet. Weil keine großen Abweichungen der Position auftreten, ist die zugehörige Linearisierung eine ziemlich gute Annäherung.
Anders sieht es aus, wenn man das Pendel im oberen, instabilen Gleichgewicht startet und dieselbe Kraft kurz anwendet. Dann wird das Pendel nach unten schwingen und sich im unteren Gleichgewicht einpendeln. Wegen der großen
Abweichungen der Position zur Startposition ist die Linearisierung für das obere Gleichgewicht keine gute Annäherung.
Systemverbindungen und Blockdiagramme
Modularität ist eines der wichtigsten Konzepte bei der Modellierung von dynamischen Systemen. Komplexe Modelle werden durch Verbindung einfacher Systemkomponenten in einer Art Hierarchie verbunden. Die Verbindung geschieht dabei durch Gleichsetzung von Signalen.
Vorteile der Modularität:
Benutzung von Softwarebibliotheken mit Standard-Systemkomponenten und Schnittstellen zwischen verschiedenen physikalischen Bereichen
Benutzung von Modellierungspaketen (MATLAB, Modelica)
Übersichtlichkeit auch bei komplexen Modellen durch die hierarchische, verschachtelte Struktur
Veränderung von einzelnen Komponenten, ohne das Gesamtgefüge zu zerstören
Beispiel: Beim inversen Pendel geht man davon aus, dass die Kraft des Wagens durch einen elektrischen Gleichstrom-Motor an einem Rad mit Radius \(r\) erzeugt wird. Wenn die Spannung \(V\) an den Motor angelegt
wird, dann erzeugt der Strom in den Spulen ein Drehmoment. Wenn \(T\) das Lastmoment des Motors ist, dann wird die Dynamik des Motors durch \(J\ddot {\phi } + b\dot {\phi } = k_m I - T\), \(L\dot {I} + RI = V -
k_e\dot {\phi }\) beschrieben, wobei \(J, b, k_m, L, R, k_e > 0\) konstant sind. Man nimmt an, dass das Lastmoment und der Winkel der Motorwelle durch \(T = Fr\) und \(p = r\phi \) mit \(F\) und \(p\)
zusammenhängen. Diese Gleichungen muss man nun mit der ursprünglichen DGL des inversen Pendels kombinieren. Man erhält dann \(L\dot {I} + RI + \frac {k_e}{r}\dot {p} = V\),
\(\left (M + m + \frac {J}{r^2}\right )\ddot {p} - m\ell \cos (\theta )\ddot {\theta } + \left (c + \frac {b}{r^2}\right )\dot {p} + m\ell \sin (\theta )\dot {\theta }^2 - \frac {k_m}{r}I =
0\) sowie
\(-m\ell \cos (\theta )\ddot {p} + m\ell ^2\ddot {\theta } + \gamma \dot {\theta } - mg\ell \sin (\theta ) = 0\).
Die gekoppelten Gleichungen heißen oft auch beidseitig gekoppelt, weil sich die Dynamik beider Systeme gegenseitig beeinflusst. Für \(k_e = 0\) wäre die
Kopplung einseitig (die erste Gleichung könnte dann separat gelöst werden).
In der Simulation erkennt man, dass für kleines \(L\) (Motor kann die Kraft schnell aufwenden) die Lösung sich kaum von der Lösung ohne Motor unterscheidet. Für größeres \(L\)
(nur langsame Aufwendung der Kraft) unterscheiden sich die beiden Systeme jedoch erheblich.
Reihenschaltung: Die Reihenschaltung (series interconnection) der Systeme
\(\dot {x}_1 = f_1(x_1, u_1)\), \(y_1 = h_1(x_1, u_1)\) und \(\dot {x}_2 = f_2(x_2, u_2)\), \(y_2 = h_2(x_2, u_2)\) erhält man, wenn man den Ausgang des ersten Systems mit dem Eingang des zweiten
Systems verbindet, also \(u_2 = y_1\) (dabei müssen die Dimensionen übereinstimmen). Man erhält das System
\(\dot {x} = f(x, u_1)\), \(y_2 = h_2(x_2, h_1(x_1, u_1))\), wobei \(x := \smallpmatrix {x_1 \\ x_2}\) und \(f(x, u_1) := \smallpmatrix {f_1(x_1, u_1) \\ f_2(x_2, h_1(x_1, u_1))}\).
Für lineare Systeme \(\dot {x}_1 = A_1 x_1 + B_1 u_1\), \(y_1 = C_1 x_1 + D_1 u_1\) und
\(\dot {x}_2 = A_2 x_2 + B_2 u_2\), \(y_2 = C_2 x_2 + D_2 u_2\) entspricht dies \(\dot {x} = Ax + Bu_1\), \(y_2 = Cx + Du_1\)
mit \(x := \smallpmatrix {x_1 \\ x_2}\) sowie \(A := \smallpmatrix {A_1 & 0 \\ B_2 C_1 & A_2}\), \(B := \smallpmatrix {B_1 \\ B_2 D_1}\), \(C := \smallpmatrix {D_2 C_1 & C_2}\) und \(D :=
D_2 D_1\).
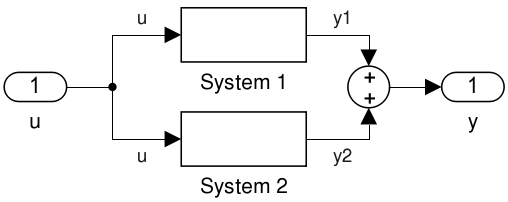
Parallelschaltung: Die Parallelschaltung (parallel interconnection) der Systeme
\(\dot {x}_1 = f_1(x_1, u_1)\), \(y_1 = h_1(x_1, u_1)\) und \(\dot {x}_2 = f_2(x_2, u_2)\), \(y_2 = h_2(x_2, u_2)\) erhält man, wenn beide denselben Eingang haben und man die Ausgänge
summiert, also \(u_1 = u_2 = u\) und \(y = y_1 + y_2\) (dabei müssen die Dimensionen übereinstimmen). Man erhält das System
\(\dot {x} = f(x, u)\), \(y = h_1(x_1, u) + h_2(x_2, u)\), wobei \(x := \smallpmatrix {x_1 \\ x_2}\) und \(f(x, u) := \smallpmatrix {f_1(x_1, u) \\ f_2(x_2, u)}\).
Für lineare Systeme \(\dot {x}_1 = A_1 x_1 + B_1 u_1\), \(y_1 = C_1 x_1 + D_1 u_1\) und
\(\dot {x}_2 = A_2 x_2 + B_2 u_2\), \(y_2 = C_2 x_2 + D_2 u_2\) entspricht dies \(\dot {x} = Ax + Bu\), \(y = Cx + Du\)
mit \(x := \smallpmatrix {x_1 \\ x_2}\) sowie \(A := \smallpmatrix {A_1 & 0 \\ 0 & A_2}\), \(B := \smallpmatrix {B_1 \\ B_2}\), \(C := \smallpmatrix {C_1 & C_2}\) und \(D := D_1 + D_2\).
Control System Toolbox: Die Control System Toolbox von MATLAB stellt sog. ss-Objekte bereit, die lineare Systeme darstellen. Die Verwendung erfolgt wie folgt:
Definition: sys = ss(A, B, C, D)
Reihenschaltung: sys = sys1 * sys2
Parallelschaltung: sys = sys1 + sys2
Simulation: y = lsim(sys, u, T, x0)
Bestimmung der definierenden Matrizen: [A, B, C, D] = ssdata(sys)
Die überladenen Operatoren * und + erinnern an die zugehörigen Operationen der Matrizen, die bei der Bildung der Reihen- bzw. Parallelschaltung verwendet werden.
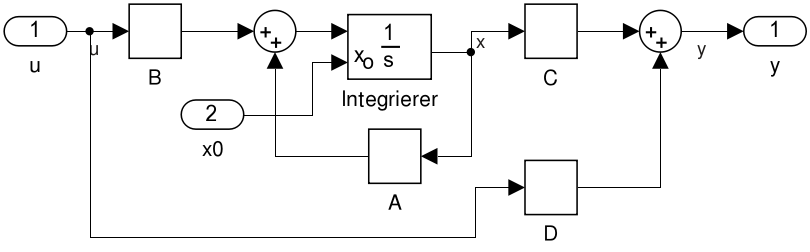
Blockdiagramm: Ein Blockdiagramm (block-diagram) besteht aus Verbindungen von einzelnen Blöcken. Solche Diagramme sollten bestimmten algebraischen Gleichungen entsprechen.
Beispiele: